1. Overflow caused by arithmetic operations on signed/unsigned integer
This is the place where most of overflow happens when do arithmetic operation on integers. In both LLP64 and LP64 [1], they have 32-bits in memory. For unsigned integer [0, 2^32 -1], roughly 0~4 billion, and [-2^31, 2^31-1], roughly -2 billion~2 billion.
Nowadays billions of data are becoming quite common. I have encountered data with size of billions in quite a few occasions. And in modern computer (PC) with 8 core and at least and 16+G memory, billions of data are no long a big problem. With multi-threading/processes application billions data can be processed within seconds.
In such application overflow can happen if you use most of the data type in your program as "int" and do arithmetic operations on them. (It does provide the temptation because by default C++ will take data as "int" and still it is one of the data type that the CPU operates most efficient on.)
The overflow could happen in such cases:
- subtraction between two unsigned/singed integers or between one signed and one unsigned
- Sum up a series of integers
- Big number number multiplication.
Problems 1:
std::vector<int> myData;
GetData(myData); // feed the data
int sum = 0;
for (int i = 0; i != myData.size(); ++i) {
sum += myData[i];
}
*) sum could be easily overflow given the value and size of myData
*) i could overflow given the size of myData, like billions
*) Most compilers will generate the warning for "i != myData.size()" to complain about the comparison between signed and unsigned integer.
Tips:
*) Promote the data type for the result of arithmetic operation. For instance to declare sum as "long long"/std::size_t.
*) Use std::size_t instead of unsigned long/unsigned long long for compatibility issue across platforms (LP64 and LLP64)
*) Use std::pdiff_t instead of long/long long for compatibility issue across platforms (LP64 and LLP64)
*) std::size_t and std::pdiff_t are defined by C++ standard and in 64 bit system they are defined as 64-bit unsigned/signed integer respectively.
The code sould be look like:
std::vector<int> myData;
GetData(myData); // feed the data
std::pdiff_t sum = 0;
for (std::size_t i = 0; i != myData.size(); ++i) {
sum += myData[i];
}
Problem 2:
If you have to do arithmetic operation between singed/unsigned integer, the best option is to promote them into std::size_t and std::pdiff_t. Considering with the range they can represent, it is safe to prevent overflow by using them in most applications.
But do keep the data type as small as possible. If the data is only 12 bits, then short should be enough. This will save you tons of memory if the this is a big data application. Just keep in mind the possible data size of the intermediate/final result during the arithmetic operations.
2. double - Machine epsilon
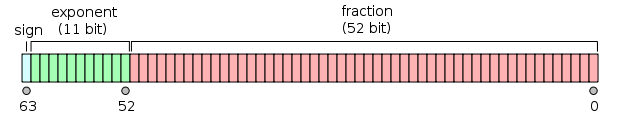
Under IEE754 double in C++ has 64 bits in memory. Top bit for sign, the following 11 bits for exponent and the rest 52 bits is for fraction. So the resolution for double is ~10^-16 (2^-53 or 2^-52).
Bits of double [2]
In c++ you can get the machine epsilion bydouble GetMachineEpsilon()
{
double epsilon = 1.0d;
while ((1.0+epsilon) != 1.0) {
epsilon/=2;
}
return epsilon;
}
The machine epsilon makes a lot of senses for some of the applications you do.
Problem: Optimization
If you are doing an optimization process. Most commonly a cost function, the variable constraints and algorithm specifications should be defined. One of most important specifications is the tolerance (termination condition and so on), which include the absolute tolerance, relative tolerance, Taylor error tolerance and so on.
Among them absolute tolerance and relative tolerance are used as termination conditions. Because of absolute tolerance is totally depends on the problem (scale), the relative tolerance can be very importance to determine if the local/global optimum is reached. Based on the numerical difference between the current and the previous iteration, it is really makes no sense to make the relative tolerance less than machine epsilon. Otherwise the termination condition could never been met and the iteration could never stop.
Problem: Simulation
If you see the difference between the current and the previous iteration becoming less and less and converging to ~10^12 (which most like taken as zero in numerical calculation, close enough to machine epsilon), this may be signalling that you can stop the process of simulation. Because this process may not be able to make any progress towards the direction of your expectation.
Tips: be aware of machine epsilon when you setting tolerance in your application
3. double - floating point underflow
This is might be the most dangerous numerical error that could impact the numerical accuracy significantly. As it is shown on Section 2 how to get machine epsilon, assume that we have a large list of very small numbers which are less than the machine epsilon. And we do addition operation of "1.0" to this full list. The final result will be "1" rather than the value it shoudl be. All the really small value in the whole list will be lost.
Here is this piece of code:
std::vector<double> val(10^9, 10^-17);
double sum = 1.0;
for (size_t i = 0; i != val.size(); ++i) {
sum += val[i];
}
We can calculate that sum of val should be 10^9*10^-17 = 10^-8. So theoretically the sum should be equal to 1.00000008. But in practice sum will be 1.0. No matter how many such numbers are added into 1.0, the result will never change and always be 1.0.
Why can this happen?
This is due to how double is represented in memory in C++. Any double value in C++ is normalized, which means that the fraction section (bottom 52 bits) is to represent a factional number between 0~1. More preciously shoue be [0.5, 1). And the exponent seciton is to present the power of 2.
For instance 0.25 will be presented as 0.5*2^-1, so the fraction will be 0.5 and the exponent will be -1. 1.0 will presented as: all fraction section set as 1 and the exponent section will be 0.
When doing the add operation on two double numbers, the small number will shift the fraction section in the right direction in order to increase the exponent section until it is equal to the exponent section of the bigger number. Then add two fraction section together. Finally this number will be normalized to make sure fraction section is bounded within [0.5, 1.0) by shifting in the right direction to increase the exponent section[3].
For instance (a=0.75) + (b=0.5*2^-53).
0.75: fraction seciton- 1100 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
exponent seciton- 0
0.5*2^-17: fraction section - 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
exponent section- -53
When do addition operation:
*) a > b
*) b's fraction section shift in the right direction to increase b's exponent section
- b's fraction section has to shift right for 53 (0 - (-53)) bit in order to b's exponent section = a's exponent section
- b's fraction section will become "0" after shift right 53 bits.
*) Adding a's and b's fraction sections together will not affect anything, and the sum is simply equal to a's fraction section because b's fraction section is equal to 0 now after shifting.
Hence underflow happens on this addition.
Fix: sum the small values first and then add the sum with the big value
As we can see above the real problem happening here is that the shifting operation to make sure the big number and the small number to have the same exponent section causes the smaller number lost its significance.
std::vector<double> val(10^9, 10^-17);
double sum = 0.0;
for (size_t i = 0; i != val.size(); ++i) {
sum += val[i];
}
sum +=1.0;
This will give the correct answer - 1.00000008
4. double - floating point overflow
The real danger here is not on the addition operation but the multiplication operation. The multiplication operation is simpler than addition operation.
*) Add the exponent sections of both numbers
*) Multiply the fraction sections
*) Normalize the number to make sure fraction seciton is bounded wiht [0.5, 1.0), by shifting fraction section and decreasing the exponent section.
So far I have no encounter with any overflow by these two operation yet in my daily work.
One more danger is the division, when big number is divided by a really small number, for say close to zero. In C++ standard it will generate std::NaN/std::Inifinite if divided by zero.
Tips for overflow:
Model the problem with a scaler if all the number are really huge. Define the bound for all variables. If the value of variable is really small, consider add/perturb machine epsilon to it in order to make sure divided-by-zero not happening.
5. Consider using data encoding techniques
If the data is really huge number and the size is quite big, data encoding techniques should be considered. It will not only save the space but also boost the performance.
For instance using simple (average value + difference) to represent very compact data. This could reduce the bits of data type from representing the whole range of data to representing the difference only. The data type could move from "int" to "short". Then half the memory is save.
Besides doing arithmetic operations on small numbers is cheap on bigger numbers. For instance working out 3+5 is cheaper than working out 231338393+9887867.
Bibliography:
[1] http://en.wikipedia.org/wiki/64-bit_computing
[2] http://en.wikipedia.org/wiki/Double_precision
[3] Donald E. Knuth "The Art of Computer Programming", Volume 2, Fundamental Algorithm, Third Edition
No comments:
Post a Comment